Modelli di regressione: scegliere quello giusto per l’analisi dei dati

L’analisi della regressione è una tecnica fondamentale per analizzare le relazioni tra variabili

Ma quale modello implementare per ottenere il miglior fit con il nostro dataset?

Regressione: una breve storia

Il termine “regressione” deriva da alcune osservazioni compiute da Sir Francis Galton nel XIX secolo.

Galton coniò il termine “regressione verso il centro” o “regressione verso la media” nel contesto di uno studio statistico sulla correlazione tra le altezze dei genitori e quelle dei figli. Notò che, in media, i figli di genitori molto alti tendevano ad essere meno alti dei loro genitori, mentre i figli di genitori molto bassi tendevano ad essere più alti dei loro genitori.

Tuttavia Sir Galton non era interessato a sviscerare il senso matematico dell’affermazione, intendendo dal suo punto di vista descrivere un fenomeno di natura prettamente biologico.

Il concetto di regressione è stato in seguito generalizzato (Yule 1897, Pearson 1903) in statistica per descrivere qualsiasi relazione predittiva tra una variabile dipendente e una o più variabili indipendenti.

In via informale il termine “regressione” viene utilizzato oggi per rifarsi al processo di costruzione di un modello statistico che descrive la relazione tra una variabile dipendente e una o più variabili indipendenti. Talvolta anche in via più semplicistica intendendo espressamente la “linea di intercetta dei minimi quadrati”.

Contestualizzando i modelli di regressione dal punto di vista analitico, il primo approccio, usando il metodo dei minimi quadrati (OLS, “Ordinary Least Squares”), si deve probabilmente a Carl Friedrich Gauss.

Gauss applicò il metodo dei minimi quadrati nel 1809, riuscendo nel tentativo di determinare l’orbita dei pianeti attorno al sole sulla base di osservazioni astronomiche già accantonato da Eulero nel 1750. Tuttavia Gauss, forse proprio con la volontà di fugare eventuali dubbi sulla paternità del suo approccio nei confronti di Legendre (1805), sancì di conoscere il metodo già dalla fine del 1700.

Formalmente questo tipo di analisi prende il nome di “Analisi di Regressione”.

Analisi di regressione

Partendo da questo presupposto, spostiamoci ora verso l’effettiva necessità operativa.

Avendo un set di dati, vorremmo capire in che modo le variabili presenti sono tra loro correlate e, soprattutto, come una o più variabili indipendenti possono influenzare una variabile dipendente di interesse. La regressione si presenta quindi come uno strumento fondamentale per modellare, analizzare e prevedere relazioni tra variabili, fornendo non solo una rappresentazione matematica di tali connessioni, ma anche intuizioni preziose per prendere decisioni informate.

In altre parole, attraverso un modello di regressione, possiamo rispondere a domande quali:

1. 1. Come varia la variabile 𝑌 al variare della variabile 𝑋?
   2. Quanto è forte l’associazione tra queste variabili?
   3. È possibile prevedere il valore di una variabile sulla base delle altre?

L’importanza dei modelli di regressione non si limita alla mera comprensione delle relazioni tra variabili.

Essi rappresentano un ponte tra i dati e l’interpretazione pratica, consentendo di tradurre insiemi complessi di osservazioni numeriche in risposte concrete.

Perché utilizzare un modello di regressione?

L’utilizzo di un modello di regressione non si limita alla sua capacità predittiva, ma si estende anche alla possibilità di:

1. Identificare relazioni significative: capire se e come alcune variabili influenzano il fenomeno osservato.
2. Quantificare gli effetti: determinare l’entità dell’effetto di una variabile indipendente sulla variabile dipendente.
3. Effettuare previsioni: utilizzare il modello per stimare valori futuri della variabile dipendente.
4. Supportare decisioni strategiche: fornire un supporto quantitativo per decisioni basate su dati.

Ad esempio, in un contesto finanziario, un modello di regressione potrebbe essere utilizzato per stimare il rendimento atteso di un portafoglio di investimenti in funzione di variabili macroeconomiche, mentre in un contesto industriale potrebbe servire a prevedere il consumo energetico sulla base della produzione giornaliera.

Nei prossimi paragrafi esploreremo diversi tipi di modelli di regressione, partendo dai più semplici e intuitivi, come la regressione lineare semplice, fino ad arrivare a modelli più avanzati, capaci di catturare relazioni non lineari e comportamenti probabilistici.

Modelli di regressione lineare semplice

La regressione lineare semplice rappresenta il modello più elementare nell’ambito dell’analisi di regressione ed è spesso il punto di partenza per comprendere concetti più avanzati.

Questo modello viene utilizzato per descrivere la relazione tra due variabili: una variabile indipendente (o esplicativa), solitamente indicata con X, e una variabile dipendente, indicata con
X. L’obiettivo principale è stimare come varia Y al variare di X.

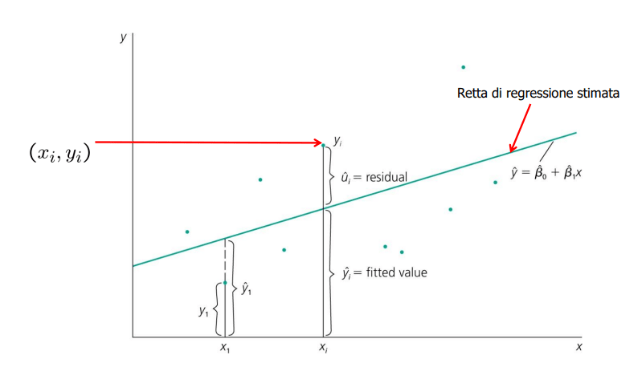
La rappresentazione analitica del modello di regressione lineare semplice si rappresenta analogamente ad una retta sul piano (effettivamente, è cioè che si va rappresentando):

Y = β0 ​+ β1​X1 + ϵ

Dove:

1. Y è la variabile dipendente.
2. X è la variabile indipendente (il fattore esplicativo).
3. β0​ è l’intercetta del modello (il valore di Y quando X=0).
4. β1​ è il coefficiente di regressione: misura la variazione media di Y per un incremento unitario di X.
5. ϵ rappresenta il termine d’errore, che cattura la variabilità di Y non spiegata dalla relazione lineare con X.

Stima dei parametri del modello di regressione lineare semplice

Il metodo più comune per stimare i parametri β0 e β1 è il metodo dei minimi quadrati ordinari (Ordinary Least Squares, OLS).

Questo metodo cerca di minimizzare la somma dei quadrati degli scarti tra i valori osservati di Y e i valori stimati dal modello.

Formalmente, gli stimatori OLS sono la soluzione al seguente problema di ottimizzazione:

Mentre la stima dei parametri β0 e β1, note alcune elementari funzioni di statistica descrittiva (covarianza tra X e Y, varianza di X, media di X e Y), è pari a:

I parametri della regressione lineare semplice possono essere anche stimati mediante un banale foglio di calcolo Excel con la formula =REGR.LIN.

Ancora più semplicemente, semplicemente plottando i valori di X e Y in un grafico di dispersione e inserendo una linea di tendenza lineare si può ottenere la rappresentazione grafica della regressione lineare (ed eventualmente anche non lineare attraverso un polinomio di grado a scelta), con il rispettivo valore R-quadro.

Se stai cercando altre formule Excel per l’analisi dei dati, ti consiglio la lettura del nostro articolo dedicato: Excel: le formule indispensabili per l’analisi dei dati

Assunzioni OLS

La validità del modello di regressione lineare semplice sottostà ad alcune assunzioni fondamentali, note come assunzioni OLS per il modello di regressione.

1. Linearità: esiste una relazione lineare tra X e Y.
2. Indipendenza degli errori: gli errori 𝜖 sono indipendenti tra loro.
3. Omogeneità della varianza (omoschedasticità): la varianza degli errori è costante per ogni valore di X.
4. Normalità degli errori: gli errori seguono una distribuzione normale con media zero.

Approfondendo le assunzioni OLS (nella loro accezione estesa) potremmo arrivare a citare il Teorema di Gauss-Markov che sancisce che se valgono le assunzioni OLS estese, allora gli stimatori OLS sono i più efficienti in assoluto tra tutti gli stimatori possibili (BLUE – Best Linear Unbiased Estimator).

Bontà del modello di regressione

Una volta stimati i parametri, è essenziale valutare l’efficacia del modello.

Gli strumenti principali includono:

1. R-quadro: indica la proporzione della varianza di Y spiegata dal modello. Varia tra 0 (nessuna relazione) e 1 (relazione perfetta).
2. Analisi dei residui: i residui (gli errori stimati) devono soddisfare le ipotesi del modello (normalità, omoschedasticità, indipendenza).
3. Significatività statistica dei coefficienti: attraverso test t si verifica se β1 sia significativamente diverso da zero.

Il modello di regressione lineare semplice è molto versatile e di immediata stima, tuttavia:

1. Può catturare solo relazioni lineari tra variabili.
2. È sensibile agli outlier (valori anomali), che possono distorcere le stime dei coefficienti.
3. Non può modellare relazioni complesse o non lineari.

Per superare queste limitazioni, è spesso necessario ricorrere a modelli più sofisticati, come la regressione lineare multipla o modelli non lineari

Modelli di regressione lineare multipla

I modelli di regressione lineare semplice (con un solo regressore) sono particolarmente esposti al problema delle variabili omesse (OVB – Omitted Variable Bias).

In via generale un modello avrà sempre delle variabili omesse (per questo motivo è fondamentale la presenza del termine d’errore), tuttavia la variabile omessa diventa particolarmente problematica, ossia, distorsiva, quando:

1. La variabile omessa contribuisce è correlata sia con la variabile dipendente Y che con una o più variabili dipendenti X (contribuisce a un effetto distorsivo indiretto).
2. La variabile omessa ha un impatto significativo sulla variabile dipendente.
3. La correlazione tra la variabile omessa e X è elevata.

Si possono pensare molteplici casi di variabili omesse.

Un caso particolarmente rappresentativo potrebbe essere stimare i voti di una scuola privata in base al numero di piatti presenti in mensa.

Naturalmente la variabile omessa è la ricchezza della scuola privata. Ma non proverei a suggerire a un rettore di aumentare i piatti in mensa per vedere migliorare i voti degli studenti!

Per ovviare a questo problema, oltre a altre specifiche di natura più puntuale (es. variabili strumentali), è bene inserire nel modello le variabili omesse.

Da un modello di regressione a una sola variabile otteniamo quindi un modello a più variabili nella forma:

Y = β0 ​+ β1​X1 + β2X2 +…+ βk​Xk + ϵ

Rispetto al modello di regressione semplice si richiedono assunzioni OLS estese (es. assenza di multicollinearità perfetta) e la stima dei regressori, pur restando fedele ai minimi quadrati ordinari, diventa più complessa (forme matriciali e calcoli più laboriosi se l’intento è eseguirli manualmente).

Modelli di regressione non lineare

Nella definizione di un modello di regressione l’esperienza dell’analista è fondamentale.

Non è possibile approcciarsi in modo dogmatico all’analisi semplicemente applicando formule e modelli in modo asettico, ma occorre immergersi nel dataset e conoscerlo e capirlo intimamente.

Intuire la relazione tra le variabili è un punto d’inizio fondamentale. Detto altrimenti, è talvolta possibile “a occhio” intuire la relazione tra la variabile dipendente oggetto di stima e le variabili indipendenti.

Meno ottimisticamente, altre volte è quantomeno intuibile o se non altro ipotizzabile la relazione tra Y e X non sia lineare, ma ad esempio esponenziale, logaritmica, polinomiale.

Se una regressione tra Y e X non è lineare:

1. L’effetto marginale di X su Y non è costante.
2. La capacità predittiva di Y* (il valore stimato) è debole, se non palesemente errato.

Il modello di regressione non lineare ha la forma:

Motivazioni per l’uso di modelli di regressione non lineare

1. Rendimenti o ritorni non lineare: il salario di un lavoratore aumenta con l’anzianità, ma fino a un certo punto. Dopo una certa età ragionevolmente potrebbe decrescere.
2. Crescite o decrescite esponenziali o logaritmiche: ad esempio la crescita di una popolazione o il decadimento delle proprietà di un elemento o una sostanza.
3. Maggiore flessibilità del modello: la complessità del mondo reale non può essere espressa con una linea retta.

Tuttavia questo non vuol dire che un modello di regressione non lineare sia sempre preferibile.

Occorre appunto avere sensibilità sul dataset. Il modello potrebbe essere ottimale sui dati di test, ma debole in un contesto predittivo (overfitting).

In via generale comunque i modelli di regressione ulteriori rispetto al modello di regressione lineare semplice sono più complessi da stimare e richiedono risorse aggiuntive.

Esiste quindi sempre un trade-off tra costi e benefici del lavoro dell’analista.

Modelli di regressione con variabile dipendente binaria

Se la variabile dipendente è binaria, ossia ammette solo due valori (0, 1) (ad esempio, maschio o femmina, accettato o rifiutato, vero o falso, etc.), ha poco senso modellare stime che possano assumere valori fuori da questo range.

In questo caso è opportuno allora ricorrere a modelli di regressione che si muovano solo all’interno di [0, 1].

I due modelli principali in questo ambito di applicazione sono i modelli Logit e Probit.

Modello di regressione probit

Il modello di regressione probit può essere formalmente definito come:

Pr(𝑌𝑖 = 1|𝑋1𝑖 , 𝑋2𝑖 , … , 𝑋𝑘𝑖) = Φ(𝛽0 + 𝛽1𝑋1𝑖 + 𝛽2𝑋2𝑖 + ⋯ + 𝛽𝑘𝑋𝑘i)=

P(𝑌𝑖 = 1) = Φ(𝛽0 + 𝛽1𝑋1𝑖 + 𝛽2𝑋2𝑖 + ⋯ + 𝛽𝑘𝑋𝑘i)

Dove:

1. La variabile dipendente Y è binaria e assume solo valori 0 e 1.
2. Φ è la funzione di densità cumulata di una normale standard.
3. X1, X2, … , X𝑘 sono i regressori inclusi nel modello.

Modello di regressione logit

l modello di regressione logit è molto simile a quello probit, con la sola differenza che la funzione di densità cumulata è quella della distribuzione logistica (indicata come 𝐹(.)) anziché quella della normale standard.

Il logit può essere formalmente definito come:

Pr(𝑌𝑖 = 1|𝑋1𝑖 , 𝑋2𝑖 , … , 𝑋𝑘𝑖) = F(𝛽0 + 𝛽1𝑋1𝑖 + 𝛽2𝑋2𝑖 + ⋯ + 𝛽𝑘𝑋𝑘i)

ovvero analogamente:

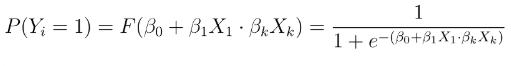
Dove:

1. La variabile dipendente Y è binaria e assume solo valori 0 e 1.
2. F è la funzione di densità cumulata di una distribuzione logistica.
3. X1, X2, … , X𝑘 sono i regressori inclusi nel modello.

Stima dei modelli probit e logit

La stima dei modelli probit e logit avviene mediante il metodo della massima verosomiglianza MLE (Maximum Likelihood Extimation).

Questa procedura richiede metodi iterativi, come l’algoritmo di Newton-Raphson.

Per i modelli logit e probit, l’R2 non costituisce una misura adeguata della loro bontà in quanto, in presenza di regressori continui, non può raggiungere il suo massimo teorico di 1 (ossia quando il modello riesce a spiegare tutta la varianza di Y).

In questi casi si può utilizzare lo 𝑝𝑠𝑒𝑢𝑑𝑜−𝑅2 , che è il rapporto tra la funzione di log-verosimiglianza del modello stimato e quella di un probit “bernoulliano” (senza regressori).

Modelli di regressione: scegliere quello giusto per l’analisi dei dati

Ci sarebbe moltissimo da dire sui modelli di regressione e un intero libro permetterebbe appena di trattare i temi introduttivi.

Impensabile quindi di esaurire il tema in un articolo.

L’ingrediente segreto di un buon modello di regressione è quello che mette insieme sia la parte “dura” di rigore matematico, robustezza del modello, controllo degli errori, metodi di stima efficaci e corretti verso errori di calcolo, variabili omesse, multicollinearità, endogeneità etc., con la conoscenza di dominio dell’analista, l’intuito, l’attenzione al significato dei risultati.

Con queste attenzioni, è possibile compiere lavori significativi con un buon potere predittivo.

Viceversa, applicando in modo asettico regole e concetti, si rischia di fare la fine di David Leinweber:

“Leinweber ha passato al setaccio un dataset delle Nazioni Unite contenente i dati economici di 140 Paesi. Ha scoperto che la produzione di burro in Bangladesh spiegava il 75% della variazione dell’indice S&P 500. Non contento, ha scoperto che se avesse aggiunto una categoria più ampia di prodotti lattiero-caseari globali, la correlazione sarebbe salita al 95%. Poi aggiunse una terza variabile, la popolazione di pecore, e scoprì che aveva spiegato il 99% della variazione dell’indice S&P 500 per il periodo 1983-1999.” [1]

Modelli di regressione: e adesso?

Vuoi approfondire qualche aspetto di questo articolo o vuoi un supporto per ottimizzare i tuoi modelli? Contattaci!